11

Pengenalan Vektor dalam Rn (Ruang Berdimensi n)

Berdasarkan konsep vektor pada Ruang berdimensi 2 dan 3 , jika kita meninjau sebuah vektor ( misalkan 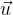 ) pada  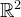maka dapat dinyatakan sebagai pasangan bilangan terurut  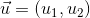begitu pula jika pad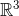a  maka .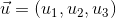

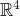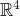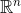Sekarang bagaimana dengan vektor yang berada di ,  dan seterusnya? Mengenai hal ini, pada abad ke-19 para ahli matematika dan ahli fisika mengembangkannya secara analitis pada ,  bahkan sampai . Kenapa perlu dikembangkan? salah satunya karena pada Sistem Persamaan Linear, dimana sebuah garis dapat dikatakan sebagai vektor yang panjangnya tak terbatas, diilustrasikan sebagai berikut :

Permasalahan timbul jika pada sistem persamaan linearnya mempunyai 4, 5 bahkan sampai n variabel, lalu bagaimana dengan vektornya? itulah mengapa perlunya generalisasi konsep dari vektor 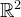 atau 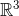 ke ruang yang lebih tinggi. Untuk masalah visualisasi secara geometri pada ruang 4, 5 dan seterusnya. “tidak” dapat dilaksanakan. Sebab dunia dimana kita hidup hanya disusun dari konsep tiga dimensi.

Definisi Vektor di Rn

Sebuah vektor 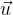 di 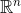 didefinisikan sebagai n-tupel bilangan riil  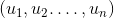dengan n adalah bilangan bulat positif. Contohnya pada  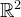vektor  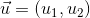dan pada  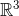vektor .

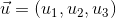Jika kita perhatikan pada gambar sebelumnya, jelas bahwa pasangan 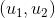 dan  tripel  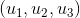tidak hanya bermakna sebagai vektor namun juga dapat berperan sebagai titik. Nah, uniknya dalam ruang-n euclides keduanya dianggap sama, hal ini berlaku juga pada 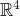,   sampai dengan 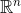. Jadi kita bebas menggambarkannya sebagai titik maupun sebagai vektor di .

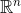Contoh :

Vektor 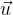 tersebut berada di .

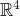Jika kita perhatikan seksama, sering muncul istilah ruang-n euclides, lalu apa sih ruang-n euclides itu ? Secara geometri, ruang euclides adalah ruang 2 atau 3 dimensi dimana aksioma-aksioma geometri euclid berlaku dengan baik, yang kemudian digeneralisasi ke dalam ruang berdimensi n. Sedangkan secara analitis, himpunan semua n-tupel bilangan real dinamakan ruang-n dan dinyatakan .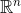

	Himpunan semua bilangan real
	Himpunan semua pasangan bilangan real
	Himpunan semua tripel bilangan real
	Himpunan semua quadrupel bilangan real
	Himpunan semua n-tupel bilangan real

Vektor Nol di Rn

Sebuah vektor di 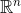 disebut sebagai vektor nol jika dan hanya jika semua entri yang didalamnya bernilai nol, biasa dituliskan sebagai berikut :

Untuk selanjutnya akan dibahas pada halaman lain mengenai operasi-operasi vektor di ruang-n euclid 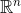. Namun sebelumnya pastikan bahwa anda sudah mengenal lebih dahulu operasi-operasi vektor pada Ruang-2 dan Ruang-3.