PENGERTIAN MATRIKS
Matriks yaitu sebuah kumpulan bilangan yang disusun dengan baris atau secara kolom atau bisa juga disusun dengan kedua – duanya dan di apit dalam tanda kurung. Elemen – elemen matriks terdiri dari bilangan – bilangan tertentu yang membentuk di dalam suatu matriks. Matriks ini sendiri digunakan sebagai menyederhana penyampaian data, sehingga akan lebih mudah untuk diolah selanjutnya.
ORDO MATRIKS
Dijelaskan sebelumnya matriks terdiri dari unsur-unsur yang tersusun secara baris dan kolom. Jika banyak baris suatu matriks adalah m, dan banyak kolom suatu matriks adalah n, maka matriks tersebut memiliki ordo matriks atau ukuran m x n. Perlu diingat bahwa m dan n hanya sebuah notasi, sehingga tidak boleh dilakukan sebuah perhitungan (penjumlahan, perkalian).
JENIS-JENIS MATRIKS
Matriks dapat dikelompokan ke beberapa jenis berdasarkan pada jumalah baris dan kolom serta pola elemen matriksnya sebagai berikut :
1. Matriks Baris dan Matriks Kolom
Matriks baris adalah suatu matriks yang hanya memiliki satu baris saja. Sedangkan, matriks kolom adalah suatu matriks yang hanya memiliki satu kolom saja.
Contoh:
A = (1 4) atau B = (3 7 9) adalah matriks baris
C =
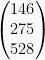 atau
atau  adalah matriks kolom
adalah matriks kolom
2. Matriks Persegi
Matriks yang memiliki jumlah kolom dan baris yang sama disebut matriks persegi. Matriks persegi memiliki ordo n.
Contoh:
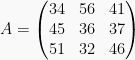 adalah matriks persegi berordo 3, atau
adalah matriks persegi berordo 3, atau 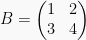 adalah matriks persegi berordo 2.
adalah matriks persegi berordo 2.
3. Matriks Segitiga Atas dan Segitiga Bawah
Matriks persegi A yang memiliki elemen matriks
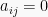
untuk

atau elemen-elemen matriks dibawah diagonal utama bernilai 0 disebut matriks segitiga atas. Matriks persegi A yang memiliki elemen matiks
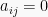
untuk
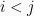
atau elemen-elemen matriks diatas diagonal utama bernilai 0 disebut matriks segitiga bawah.
Contoh:
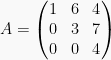
adalah matriks segitiga atas,
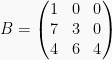
adalah matriks segitiga bawah.
4. Matriks Diagonal
Matriks persegi A yang memiliki elemen matiks
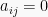
untuk

atau elemen-elemen matriks diluar diagonal utama bernilai 0 disebut matriks diagonal.
Contoh:

atau
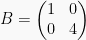
5. Matriks Skalar
Matriks diagonal yang memiliki elemen-elemen pada diagonal utamanya bernilai sama disebut matriks skalar.
Contoh:
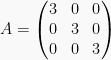
atau

6. Matriks Identitas
Matriks diagonal dengan elemen-elemen diagonal utamanya bernilai 1 disebut matriks identitas. Pada umumnya matriks identitas dinotasikan dengan “I”. Contoh:

atau
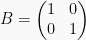
7. Matriks Simetris
Matriks persegi A yang memiliki elemen matiks baris ke-I sama dengan elemen matriks kolom ke-j untuk i = j disebut simetris. Atau, dapat dikatakan elemen
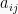
sama dengan elemen
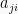
.
Contoh:
Dapat dilihat bahwa elemen baris ke-1 sama dengan kolom ke-1, baris ke-2 sama dengan kolom ke-2, dan baris ke-3 sama dengan kolom ke-3.
8.Transpose Matriks
Transpose matriks merupakan perubahan baris menjadi kolom dan sebaliknya. Transpose matriks dari

adalah sebuah matriks dengan ukuran (n x m) dan bernotasi A
T. Jika matriks A ditanspose, maka baris 1 menjadi kolom 1, baris 2 menjadi kolom 2, dan begitu seterusnya.
Contoh:
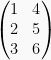
ditranspose menjadi

.
Sifat dari transpose matriks:
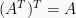
.
(Sebab elemen-elemen baris ke-1 dan ke-3 adalah sama).
(Sebab elemen-elemen baris ke-3 sama dengan kelipatan elemen-elemen baris ke-1).
4. |AB| : |A| ×|B|5. |AT| = |A|, untuk AT ialah transpose dari matriks A.6. |A–1| =, untuk A–1 ialah invers dari matriks A.
7. |kA| = kn |A|, untuk A ordo n × n dan k adalahsuatu konstanta.

